Formula per calcolare la distribuzione T di Student
La formula per calcolare la distribuzione T (che è anche comunemente nota come distribuzione T di Student) è mostrata come Sottraendo la media della popolazione (media del secondo campione) dalla media del campione (media del primo campione) che è (x̄ - μ) che è poi diviso per la deviazione standard delle medie che è inizialmente divisa per la radice quadrata di n che è il numero di unità in quel campione (s ÷ √ (n)).
La distribuzione T è un tipo di distribuzione che assomiglia quasi alla normale curva di distribuzione o curva a campana ma con una coda un po 'più grassa e più corta. Quando la dimensione del campione è piccola, verrà utilizzata questa distribuzione al posto della distribuzione normale.
t = (x̄ - μ) / (s / √n)
Dove,
- x̄ è la media campionaria
- μ è la media della popolazione
- s è la deviazione standard
- n è la dimensione del campione dato
Calcolo della distribuzione T
Il calcolo della distribuzione t di Student è abbastanza semplice, ma sì, i valori sono obbligatori. Ad esempio, è necessaria la media della popolazione, che è la media dell'universo, che non è altro che la media della popolazione mentre la media campionaria è richiesta per testare l'autenticità della popolazione significa se l'affermazione rivendicata sulla base della popolazione è effettivamente vera campione, se presente, rappresenterà la stessa affermazione. Quindi, la formula di distribuzione t sottrae la media campionaria dalla media della popolazione e quindi la divide per la deviazione standard e la moltiplica per la radice quadrata della dimensione del campione per standardizzare il valore.
Tuttavia, poiché non esiste un intervallo per il calcolo della distribuzione t, il valore può diventare strano e non saremo in grado di calcolare la probabilità poiché la distribuzione t di Student ha dei limiti di arrivare a un valore, e quindi è utile solo per dimensioni del campione più piccole . Inoltre, per calcolare la probabilità dopo essere arrivati a un punteggio, è necessario trovare il valore di quello dalla tabella di distribuzione t dello studente.
Esempi
Esempio 1
Considera le seguenti variabili che ti vengono fornite:
- Media della popolazione = 310
- Deviazione standard = 50
- Dimensione del campione = 16
- Media campionaria = 290
Calcola il valore di distribuzione t.
Soluzione:
Utilizzare i seguenti dati per il calcolo della distribuzione T.

Quindi, il calcolo della distribuzione T può essere fatto come segue:
Qui vengono forniti tutti i valori. Dobbiamo solo incorporare i valori.
Possiamo usare la formula di distribuzione t

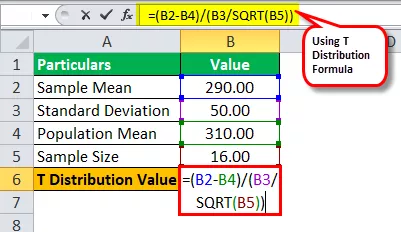
Valore di t = (290-310) / (50 / √16)

Valore T = -1,60
Esempio n. 2
La società SRH afferma che i suoi dipendenti a livello di analista guadagnano una media di $ 500 l'ora. Viene selezionato un campione di 30 dipendenti a livello di analista e il loro guadagno medio orario è stato di $ 450, con una deviazione del campione di $ 30. E supponendo che la loro affermazione sia vera, calcola il valore di distribuzione t, che deve essere utilizzato per trovare la probabilità di distribuzione t.
Soluzione:
Utilizzare i seguenti dati per il calcolo della distribuzione T.
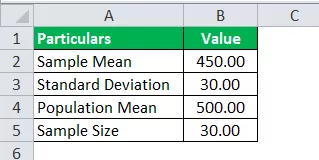
Quindi, il calcolo della distribuzione T può essere fatto come segue:
Qui vengono forniti tutti i valori; dobbiamo solo incorporare i valori.
Possiamo usare la formula di distribuzione t


Valore di t = (450-500) / (30 / √30)

Valore T = -9,13
Quindi il valore per il punteggio t è -9,13
Esempio n. 3
Il consiglio dell'università universale aveva somministrato un test di livello di QI a 50 professori selezionati casualmente. E il risultato che hanno trovato era che il punteggio medio del livello di QI era 120 con una varianza di 121. Supponiamo che il punteggio t sia 2,407. Qual è la media della popolazione per questo test, che giustificherebbe il valore del punteggio t come 2,407?
Soluzione:
Utilizzare i seguenti dati per il calcolo della distribuzione T.

Qui vengono forniti tutti i valori insieme al valore t; questa volta dobbiamo calcolare la media della popolazione invece del valore t.
Anche in questo caso, utilizzeremo i dati disponibili e calcoleremo le medie della popolazione inserendo i valori indicati nella formula sottostante.
La media campionaria è 120, la media della popolazione è sconosciuta, la deviazione standard campionaria sarà la radice quadrata della varianza, che sarebbe 11, e la dimensione del campione è 50.
Quindi, il calcolo della media della popolazione (μ) può essere eseguito come segue:
Possiamo usare la formula di distribuzione t.


Valore di t = (120 - μ) / (11 / √50)
2,407 = (120 - μ) / (11 / √50)
-μ = -2,407 * (11 / √50) -120
La media della popolazione (μ) sarà -

μ = 116,26
Quindi il valore per la media della popolazione sarà 116,26
Rilevanza e utilizzo
La distribuzione T (e i valori dei punteggi t associati) viene utilizzata nel test di ipotesi quando è necessario scoprire se si deve rifiutare o accettare l'ipotesi nulla.

Nel grafico sopra, la regione centrale sarà l'area di accettazione e la regione della coda sarà la regione di rifiuto. In questo grafico, che è un test a 2 code, il blu ombreggiato sarà la regione di rigetto. L'area nella regione della coda può essere descritta con i punteggi t o con i punteggi z. Facciamo un esempio; l'immagine a sinistra rappresenterà un'area nelle code del cinque percento (che è del 2,5% su entrambi i lati). Il punteggio z dovrebbe essere 1,96 (prendendo il valore dalla tabella z), che rappresenta la deviazione standard di 1,96 dalla media o dalla media. L'ipotesi nulla può essere rifiutata se il valore del punteggio z è inferiore al valore di -1,96 o il valore del punteggio z è maggiore di 1,96.
In generale, questa distribuzione deve essere utilizzata come descritto in precedenza quando si ha una dimensione del campione inferiore (per lo più inferiore a 30) o se non si conosce la varianza della popolazione o la deviazione standard della popolazione. Per scopi pratici (cioè nel mondo reale), questo sarebbe principalmente sempre il caso. Se la dimensione del campione fornito è abbastanza grande, le 2 distribuzioni saranno praticamente simili.








