Qual è la formula della gamma?
La formula dell'intervallo si riferisce alla formula che viene utilizzata per calcolare la differenza tra il valore massimo e il valore minimo dell'intervallo e in base alla formula il valore minimo viene sottratto dal valore massimo per determinare l'intervallo.
Intervallo = il valore massimo - il valore minimo
Del set di dati fornito, che fornisce agli statistici e al matematico una migliore comprensione del set di dati, quanto è vario. È l'approccio più semplice per calcolare la varianza nelle statistiche.
Spiegazione
È abbastanza semplice e facile da usare poiché la formula indica il valore massimo meno il valore minimo del campione dato. Pertanto, la varianza tra il valore massimo e il valore minimo è l'intervallo e, sebbene sia semplice da usare e da comprendere, richiede un'interpretazione corretta.
Ad esempio, se c'è un outliner nei dati, l'intervallo verrebbe influenzato dagli stessi e otterrebbe il risultato che porterà a false dichiarazioni. Prendiamo un esempio pratico per i dati dati 2, 4, 7, 7, 100 quindi l'intervallo sarebbe 100-2, che è 98, ma come si può vedere che l'intervallo di dati è inferiore a 10 ma considerando e interpretando quei dati è compreso tra 98 porterà a false dichiarazioni. Quindi l'interpretazione della distanza dovrebbe essere condotta con la dovuta considerazione.
Esempi
Esempio 1
Considera la seguente serie di dati 2,2,4,4, 4, 6,7,7,8, 8, 8, 9, 9, 9, 9, 9. Ti viene richiesto di calcolare l'intervallo per questo campione.
Soluzione:
- Valore massimo = 9
- Valore minimo = 2
Intervallo = 9-2
Intervallo = 7
Esempio n. 2
Mr. Stark, uno scienziato che lavora da 10 anni con un'azienda chiamata Dream moon. Il signor Arora, il suo supervisore, sta conducendo un esperimento sulla salute umana e ha raccolto pochi dati campione di statura maschile che sono 162, 158, 189, 144, 151, 150, 151, 178, 155, 160. Ora è perplesso e vuole sapere quanti dati sono variati. Il signor Stark, che è uno statistico esperto, è stato contattato dal suo supervisore, il signor Arora, per rimuovere la sua confusione riguardo alla variazione della formula. Il signor Arora è tenuto a fornire una risposta al suo supervisore; ti viene richiesto di calcolare quanto sono variati i dati?
Soluzione:
Intervallo = valore massimo - valore minimo
- Valore massimo = 189
- Valore minimo = 144
Intervallo = 189-144
Intervallo = 45
I dati o il campione raccolto hanno una variazione di 45.
Esempio n. 3
Il signor Buffet, un noto e stimato investitore in tutto il mondo, sta ora valutando le azioni del mercato statunitense e sta analizzando alcune di esse su cui desidera investire. L'elenco include le principali società blue chip negli Stati Uniti. Di seguito sono riportati i titoli oi titoli selezionati insieme al loro ultimo prezzo di mercato azionario, che è indicato in $ USA, in cui sta valutando di investire.
È necessario calcolare l'intervallo e trovare la variazione dell'elenco.
Soluzione:
Di seguito vengono forniti i dati per il calcolo dell'intervallo.
Utilizzando le informazioni di cui sopra, il calcolo del valore massimo in Excel sarà il seguente,

Valore massimo = 204,66
Calcolo del valore minimo in Excel come segue,
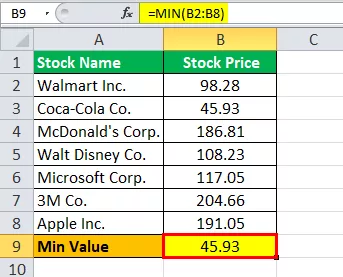
Valore min = 45.93
Pertanto, il calcolo dell'intervallo è il seguente,

Intervallo = 204,66 - 45,93
La gamma sarà -
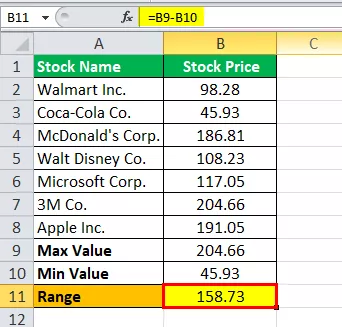
Intervallo = 158,73
Usi di Range Formula
L'intervallo, a suo modo, è molto semplice e molto basilare per capire come sono distribuiti i numeri nel dato set di dati o nel dato campione perché, come affermato in precedenza, è relativamente facile fare il calcolo in quanto c'è il richiesto solo per un'operazione aritmetica molto elementare che sottrae solo il minimo dal valore massimo, ma l'intervallo ha poche applicazioni in più per un dato set di dati o un dato campione in statistica. L'intervallo è utile anche per stimare un'altra misura dello spread, chiamata varianza o deviazione standard.
L'intervallo, come accennato in precedenza, può solo fornire informazioni sui dettagli di base, ovvero dove si troverà la diffusione di un dato campione o di un dato insieme di dati. Dando la differenza o diciamo la varianza tra i valori più alti e più bassi di un dato campione o dato insieme di dati, fornisce un'informazione o un'idea approssimativa sulle osservazioni estreme significative su quanto siano diffuse quelle, ma ancora una volta non fornisce suggerimento o qualsiasi informazione sugli altri punti di dati che dove si troverebbero, che è il principale punto debole dell'uso dell'equazione dell'intervallo.
L'intervallo, come discusso in precedenza, è utile per rappresentare la diffusione all'interno di un dato campione o di un dato insieme di dati e inoltre è utilizzato anche per confrontare la diffusione risultante tra lo stesso dato campione o gli stessi dati.








