Qual è il coefficiente di correlazione?
Il coefficiente di correlazione viene utilizzato per determinare quanto è forte la relazione tra due variabili ei suoi valori possono variare da -1,0 a 1,0, dove -1,0 rappresenta la correlazione negativa e +1,0 rappresenta la relazione positiva. Considera i movimenti relativi nelle variabili e quindi definisce se esiste una relazione tra di loro.
Formula del coefficiente di correlazione
r = n (∑xy) - ∑x ∑y / √ (n * (∑x 2 - (∑x) 2 )) * (n * (∑y 2 - (∑y) 2 ))
Dove
- r = coefficiente di correlazione
- n = numero di osservazioni
- x = 1 a variabile nel contesto
- y = 2 ° variabile
Spiegazione
Se c'è una correlazione o diciamo la relazione tra due variabili, allora deve indicare se una delle variabili cambia di valore, quindi anche l'altra variabile tenderà a cambiare di valore, diciamo nello specifico che potrebbe essere nella stessa o in nella direzione opposta. La parte numeratore dell'equazione conduce un test e la forza relativa delle variabili che si muovono insieme, e la parte denominatore dell'equazione scala il numeratore moltiplicando le differenze delle variabili dalle variabili al quadrato.
Esempi
Esempio 1
Considera le seguenti due variabili, x e y, che ti vengono richieste per calcolare il coefficiente di correlazione.
Di seguito vengono forniti i dati per il calcolo.

Soluzione:
Usando l'equazione sopra, possiamo calcolare quanto segue

Abbiamo tutti i valori nella tabella sopra con n = 4.
Inseriamo ora i valori per il calcolo del coefficiente di correlazione.

Pertanto, il calcolo è il seguente,

r = (4 * 25.032,24) - (262,55 * 317,31) / √ ((4 * 20.855,74) - (262,55) 2 ) * ((4 * 30.058,55) - (317,31) 2 )
r = 16.820,21 / 16.831,57
Il coefficiente sarà -

Coefficiente = 0,99932640
Esempio n. 2
Il Paese X è un paese a economia in crescita e vuole condurre un'analisi indipendente delle decisioni prese dalla sua banca centrale in merito alle variazioni dei tassi di interesse, indipendentemente dal fatto che abbiano avuto un impatto sull'inflazione e che la banca centrale sia in grado di controllarlo.
Di seguito si riporta il riepilogo del tasso di interesse e del tasso di inflazione che ha prevalso nella media nel paese per quegli anni.
Di seguito vengono forniti i dati per il calcolo.

Il presidente del paese si è avvicinato a voi per condurre un'analisi e fornire una presentazione sulla stessa nella prossima riunione. Usa la correlazione e determina se la banca centrale ha raggiunto il suo obiettivo o meno.
Soluzione:
Utilizzando la formula discussa sopra, possiamo calcolare il coefficiente di correlazione. Trattare il tasso di interesse come una variabile, diciamo x, e trattare il tasso di inflazione come un'altra variabile come y.

Abbiamo tutti i valori nella tabella sopra con n = 6.
Inseriamo ora i valori per il calcolo del coefficiente di correlazione.


r = (6 * 170,91) - (46,35 * 22,24) / √ ((6 * 361,19) - (46,35) 2 ) * ((6 * 82,74) - (22,24) 2 )
r = -5,36 / 5,88
La correlazione sarà:

Correlazione = -0,92
Analisi: sembra che la correlazione tra il tasso di interesse e il tasso di inflazione sia negativa, il che sembra essere il rapporto corretto. All'aumentare del tasso di interesse, l'inflazione diminuisce, il che significa che tendono a muoversi nella direzione opposta l'una rispetto all'altra, e dal risultato di cui sopra risulta che la banca centrale è riuscita ad attuare la decisione relativa alla politica dei tassi di interesse.
Esempio n. 3
Il laboratorio ABC sta conducendo ricerche su altezza ed età e voleva sapere se esiste qualche relazione tra di loro. Hanno raccolto un campione di 1000 persone per ciascuna delle categorie e hanno trovato un'altezza media in quel gruppo.
Di seguito vengono forniti i dati per il calcolo del coefficiente di correlazione.

È necessario calcolare il coefficiente di correlazione e giungere alla conclusione che se esiste una relazione.
Soluzione:
Trattando l'età come una variabile, diciamo x, e l'altezza (in cm) come un'altra variabile come y.

Abbiamo tutti i valori nella tabella sopra con n = 6.
Inseriamo ora i valori per il calcolo del coefficiente di correlazione.

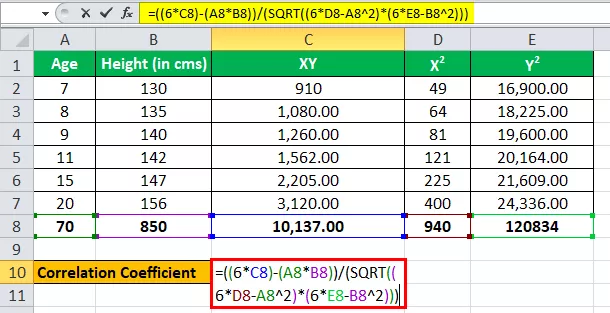
r = (6 * 10,137) - (70 * 850) / √ ((6 * 940 - (70) 2 ) * ((6 * 1,20,834) - (850) 2 )
r = 1.322,00 / 1.361,23
La correlazione sarà:

Correlazione = 0,971177099
Rilevanza e utilizzo
Viene utilizzato in statistica principalmente per analizzare la forza della relazione tra le variabili che sono prese in considerazione e inoltre misura se esiste una relazione lineare tra i set di dati dati e quanto bene potrebbero essere correlati. Una delle misure comuni utilizzate nella correlazione è il coefficiente di correlazione di Pearson.
Se una variabile cambia di valore e insieme a quell'altra variabile cambia di valore, allora comprendere quella relazione è fondamentale in quanto si può utilizzare il valore della prima variabile per prevedere il cambiamento nel valore dell'ultima variabile. Una correlazione ha molti molteplici usi oggi in questa era moderna come viene utilizzata nel settore finanziario, nella ricerca scientifica e dove no. Tuttavia, è importante sapere che la correlazione ha tre tipi principali di relazioni. La prima è una relazione positiva, che afferma che se c'è un cambiamento nel valore di una variabile, allora ci sarà un cambiamento nella variabile correlata nella stessa direzione. Allo stesso modo, se esiste una relazione negativa, la variabile correlata si comporterà nella direzione opposta. Inoltre, se non c'è correlazione, r implicherà un valore zero.Guarda le immagini sottostanti per comprendere meglio il concetto.






