Definizione di correlazione negativa
In parole povere, la correlazione negativa è una relazione tra due variabili. Fanno parte di una funzione in cui variabili dipendenti e indipendenti si muovono in direzioni diverse in termini di valore. Ad esempio, se la variabile indipendente aumenta, la variabile dipendente diminuisce e viceversa.
La correlazione negativa può essere descritta dal coefficiente di correlazione quando il valore di questa correlazione è compreso tra 0 e -1. La quantità di una correlazione negativa perfetta è -1. La forza della correlazione tra le variabili può variare. Ad esempio, supponiamo che due variabili, xey siano correlate a -0,8. Significa che quando x aumenta di 1 unità, y diminuirà di 0,8. Consideriamo ora che la correlazione negativa tra queste variabili è -0,1. In questo caso, ogni variazione di unità nel valore della variabile x risulterà in una differenza di 0,1 unità solo nel costo della variabile y.
Comprensione della correlazione negativa
Per comprendere meglio la correlazione negativa, dobbiamo avere anche una comprensione di base della correlazione. La correlazione è uno strumento statistico che misura il grado di relazione tra due diverse funzioni. Ad esempio, il peso e l'altezza di una persona. Generalmente, all'aumentare dell'altezza, aumenta anche il valore della persona. Indica che esiste una correlazione positiva tra altezza e peso perché all'aumentare di una variabile, aumentano anche altre variabili. Ma la correlazione è negativa se le due variabili si muovono in direzioni opposte, ad esempio altezza dal livello di tenuta e temperatura. All'aumentare dell'altezza, la temperatura diminuisce.
La formula fornisce la correlazione:

Qui,
- r = coefficiente di correlazione;
- = Media della variabile X;
- = Media della variabile Y
La riorganizzazione ci dà questa formula:

La correlazione può assumere qualsiasi valore compreso tra -1 e 1. Il segno negativo indica una correlazione negativa, mentre un segno positivo indica una correlazione positiva. La correlazione zero significa che non esiste alcuna relazione tra le due variabili.

Perché la correlazione negativa è importante?
- Gestione del portafoglio : la correlazione è ampiamente utilizzata nella gestione dei portafogli. Si dice spesso che i portafogli dovrebbero essere diversi. Dovrebbe consistere in più investimenti che comportano rischi e rendimenti diversi. Se abbiamo lo stesso tipo di titoli nel nostro portafoglio, qualsiasi evento importante avrà un impatto non solo su un titolo ma sull'intero portafoglio. A tal fine, troviamo una correlazione tra i rendimenti dei titoli. I depositi con correlazioni perfettamente positive non dovrebbero essere acquistati insieme. Per diversificare il portafoglio, spesso, si aggiungono le puntate con correlazioni negative. Considera l'esempio sopra discusso delle azioni delle compagnie aeree e dei prezzi del petrolio. Se un portafoglio ha azioni energetiche, la direzione può prendere in considerazione l'acquisto di azioni aeree per proteggersi dal calo dei prezzi del petrolio.
- Economia : molte tendenze associate all'economia implicano una correlazione negativa. Questa relazione tra i movimenti può essere utile per le questioni relative alle politiche economiche. Ad esempio, disoccupazione e spesa dei consumatori. Quanto all'aumento della spesa, la disoccupazione diminuisce (generalmente).
Esempi reali di correlazione negativa
- Prezzi del petrolio e azioni delle compagnie aeree: il petrolio è una delle principali materie prime per le compagnie aeree. Man mano che i prezzi del petrolio aumentano, la loro redditività inizia a diminuire, il che si riflette anche sui prezzi delle azioni. Quindi, mostrano una correlazione negativa
- Mercato azionario e prezzi dell'oro (il più delle volte, non sempre): l'oro funge sempre da opzione di investimento alternativa per gli investitori azionari. Pertanto, ogni volta che il mercato azionario sembra essere in declino, gli investitori si interessano a investire in oro e, quindi, i prezzi dell'oro iniziano ad aumentare
Esempio pratico di correlazione negativa
Supponiamo che due azioni abbiano fornito i seguenti rendimenti ogni anno nel periodo 2011-16:

Considerando i rendimenti azionari del primo titolo come variabile "x" e quello del secondo titolo come "y".
Calcolo della variabile xy
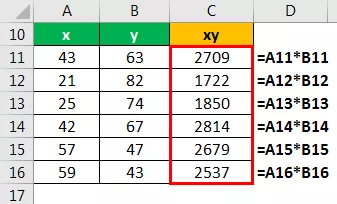
Calcolo della variabile X 2

Calcolo della variabile Y 2

Somma

Calcolo del coefficiente di correlazione (r)

- = ((6 * 14311) - (247 * 376)) / (((6 * 11409) - (247 2)) 0,5 * ((6 * 247160- (376 2)) 0,5)
- = Coefficiente di correlazione (r) = -0,97608
Fare riferimento al foglio Excel sopra riportato per il calcolo dettagliato.
Il valore negativo del coefficiente di correlazione mostra che le variabili sono correlate negativamente.
Conclusione
A volte, possono essere coinvolti altri fattori che inducono le variabili a comportarsi in un modo particolare. Nell'esempio discusso sopra, si può dedurre che quando x aumenta, y diminuisce. Ma sarebbe sbagliato supporre che l'aumento di "x" stia facendo diminuire la "y" perché è possibile che entrambe le società interessate siano coinvolte in attività completamente diverse e siano influenzate da condizioni economiche diverse.
Pertanto, le correlazioni dovrebbero essere utilizzate solo per determinare una causa. I dirigenti possono utilizzarlo per comprendere la relazione tra variabili, come la domanda di mercato e la spesa dei consumatori, che già esiste come parte dell'analisi. Ma non dovrebbe essere usato per indagare il cambiamento in una variabile a causa di altre variabili perché ci saranno sempre più fattori che influenzano quella relazione. Ad esempio, la spesa dei consumatori nel mercato e le entrate di un'azienda di beni di largo consumo. Possono mostrare una correlazione positiva, ma è possibile che i ricavi di quella società siano aumentati a causa di qualche altro motivo come il lancio di un nuovo prodotto o l'espansione in un'economia emergente.








