Definizione di compounding
Il compounding è il metodo di calcolo del tasso di interesse che è effettivamente interesse sugli interessi in cui l'interesse è calcolato sull'investimento / capitale iniziale più l'interesse guadagnato e altri reinvestimenti, in altre parole l'interesse guadagnato viene accumulato all'importo del capitale a seconda del periodo di deposito o prestito che può essere mensile, trimestrale o annuale
Proviamo a capire cos'è la composizione e come funziona attraverso alcuni esempi di base
I 4 migliori esempi di potere del compounding
Esempio 1
Shane e Mark hanno entrambi deciso di investire $ 1,00.000, ma Shane ha deciso di investire in interessi semplici, mentre Mark investe in interessi composti per dieci anni al 10% di interesse. Vediamo cosa succede dopo dieci anni.
Soluzione:
Quindi, il calcolo dell'investimento di Shane sarà:

Importo totale del guadagno = $ 200.000
Con un interesse semplice, Shane riceverà $ 2.00.000 dopo 10 anni.
Il calcolo dell'investimento in marchio sarà:

Importo totale del guadagno = $ 2,59,374
Con l'interesse composto, il valore degli investimenti di Mark crescerà fino a $ 2,59,374.
Ora Shane ha deciso di investire attraverso metodi di composizione come Mark, ed entrambi hanno investito $ 2,00.000 al tasso del 15%.
Il calcolo dell'investimento di Shane sarà:

Importo totale del guadagno = $ 8,09,111,55
Shane rimane investito per 10 anni e ottiene l'importo finale di $ 8,09,111,55 al tasso del 15%.
Il calcolo dell'investimento in marchio sarà:

Importo totale del guadagno = $ 65,83,790,52
Tuttavia, Mark è un investitore di pazienza a lungo termine e rimane investito per 25 anni e il suo valore di investimento cresce fino a $ 65,83,790.52
L'esempio sopra mostra il potere della composizione. Più lungo è l'orizzonte di investimento, maggiore è la crescita esponenziale.
Esempio n. 2 (settimanale)
Simon ha 7500 dollari di risparmi e per il fondo per il college di suo figlio, che andrà al college dopo 15 anni, ha deciso di investire in buoni di risparmio statunitensi. L'obiettivo di Simon è quello di risparmiare $ 20.000 e il tasso percentuale annuo per un'obbligazione di risparmio statunitense è del 6%. Qual è il valore futuro di Simon Money dopo 15 anni?
Soluzione:
Dato,
- Principale = $ 7500
- Tasso = 6% o 0,06
- Periodo di tempo = 15 anni.
- Quante volte è composto in un anno n = 52 settimane
- Valore futuro =?
Quindi, il calcolo del valore futuro sarà:

La formula per la composizione settimanale è la seguente.
F = P (1 + r / n) n * t- F = $ 7500 (1 + 0,06 / 52) 52 * 15
- F = $ 7500 (1 + 0,001153846) 780
- F = $ 18.437,45
Quindi dal calcolo di cui sopra, è chiaro che l'obiettivo di Simon di risparmiare $ 20,00 non verrà raggiunto con i metodi sopra, ma è più vicino a quello.
Metodo di compounding continuo
Ora proviamo l'esempio precedente con la formula a composizione continua.
Quindi, il calcolo del valore futuro sarà:

- F = $ 7500e 0,06 * 15
- F = $ 7500e 0,9
- Valore futuro (F) = $ 18.447,02
Ora, anche con il Continuous Compounding, l'obiettivo di Simon di risparmiare $ 20.000 per il fondo del college di suo figlio non sarà raggiunto.
Vediamo con la Formula mensile composta che quanti soldi ha dovuto investire Simon per raggiungere il suo obiettivo di risparmiare $ 20.000 in 15 anni con un TAEG del 6%?
Quindi, il calcolo del valore futuro sarà:
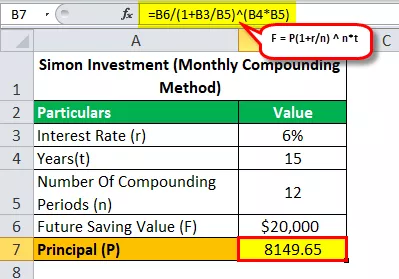
- $ 20.000 = P (1 + 0,06 / 12) 12 * 15
- P = $ 20.000 / (1 + 0,06 / 12) 12 * 15
- Principale (P) = 8149,65
Quindi, risolvendo l'equazione sopra, otterremo una risposta che è $ 8.149,65 (importo, che Simon deve investire per raggiungere il suo obiettivo di risparmiare $ 20.000 in 15 anni).
Esempio n. 3 (rendimento annualizzato effettivo)
Supponiamo che la banca limitata XYZ dia il 10% all'anno agli anziani per un deposito fisso, e assumiamo qui che l'interesse bancario sia composto trimestralmente come tutte le altre banche. Calcola il rendimento annualizzato effettivo per 5, 7 e 10 anni.
Soluzione:
Rendimento annualizzato per 5 anni:
- t = 5 anni
- n = 4 (trimestrale composto)
- I = 10% annuo
Quindi A = (1 + 10% / 100/4) (5 * 4)
- A = (1 + 0,025) 20
- A = 1,6386
- I = 0,6386 in 5 anni
Interesse effettivo = 0,6386 / 5
Efficace I = 12,772% annuo
Rendimento annualizzato per 7 anni:
- t = 7 anni
- n = 4 (trimestrale composto)
- I = 10% annuo
Quindi A = (1 + 10% / 100/4) (7 * 4)
- A = (1 + 0,025) 28
- A = 1,9965
- I = 1.9965 in 7 anni
- Efficace I = 0,9965 / 7
Efficace I = 14,236% annuo
Rendimento annualizzato per 10 anni:
- t = 10 anni
- n = 4 (trimestrale composto)
- I = 10% annuo
Quindi A = (1 + 10% / 100/4) (10 * 4)
- A = (1 + 0,025) 40
- A = 2,685
- I = 1,685 in 10 anni
- Efficace I = 1.685 / 10
Efficace I = 16,85% annuo
Esempio n. 4 - (Rendite: valore futuro)
$ 1.000 vengono investiti ogni 3 mesi al 4,8% annuo composto trimestralmente. Quanto varrà la rendita in 10 anni?
Soluzione:
Quindi quando diciamo quanto varrà la rendita in 10 anni significa che qui dobbiamo trovare un valore futuro, e questo è importante perché ogni volta che c'è un esempio sulle rendite, dobbiamo vedere cosa dobbiamo scoprire.
Quindi, la formula del valore futuro è
FV di rendita = P ((1+ r) n - 1 / r)- P = pagamento periodico
- r = Tariffa per periodo
- n = Numero di periodi
Quindi la formula del valore futuro è
- Quindi qui P = $ 1.000
- r = 4,8% annuo o 0,048
- r (trimestrale) = 0,048 / 4
- r (trimestrale) = 0,012
- n = 10 anni
- n (Numero di volte in cui verrà applicata la composizione) = 10 × 4 = 40
Quindi, il calcolo del FV della rendita sarà:

Quindi ora FV = $ 1000 (1 + 0,012) 40-1 / 0,012)
Quindi risolvendo l'equazione di cui sopra otterrai un FV di $ 50.955,30
Quindi quanto sarà la rendita in 10 anni e la risposta è $ 50,955,30
Inoltre, possiamo anche scoprire dall'esempio sopra che quanti interessi si guadagnano in 10 anni.
Poiché vengono investiti 40 volte $ 1000, si tratta di un investimento totale (40 × $ 1000 = $ 40.000).
Quindi interesse = valore futuro - investimento totale
- Interesse = $ 50.955,30 - $ 40.000
- Interesse = $ 10.955,30
Quindi qui, è importante capire che nelle rendite gli investitori possono guadagnare molto interesse. Negli esempi particolari sopra, un deposito di $ 40.000 dà, in cambio, un interesse totale di $ 10.955,30.
Nota: è possibile scaricare il modello Excel fornito sopra per un calcolo dettagliato.








